[CS 스터디 : JAVA] (4) 이진 탐색 트리
이진 탐색 트리(Binary Search Tree, BST)
: 이진트리 + 조건 한개 추가(모든 노드에 대해 왼쪽 노드의 데이터 < 오른쪽 노드의 데이터)
: 모든 노드에 대해 왼쪽 노드의 데이터가 오른쪽 노드의 데이터보다 작음을 만족하는 이진 트리

: 검색 목적의 자료구조 > 중복된 키를 허용하지 않음
: 중위 순회 방식 ( 왼 - 루트 - 오)

→ 선언 방식
class BinarySearchTree {
class Node { // 노드 클래스 : 데이터, 왼쪽 노드, 오른쪽 노드
int data;
Node left, right;
public Node(int item){ // 생성자 초기화
data = item;
left = right = null;
}
}
Node root; // 루트 노드
BinarySearchTree() { root = null; } // 루트 노드가 비어있는 생성자
BinarySearchTree(int value) { root = new Node(value); } // 루트 노드를 지정한 생성자
public static void main(String[] args){
BinarySearchTree tree = new BinarySearchTree(); // 호출
}
}
(1) 원소 탐색 : 아래의 BST에서 원소 10 찾기 (위치 또는 존재 여부)

❶ 탐색 수와 루트 노드의 데이터 비교
❷ 탐색 수 > 루트 노드 : 오른쪽 트리 탐색
❷ 탐색 수 < 루트 노드 : 왼쪽 트리 탐색
❸ 계속해서 ❷ 과정을 반복하며 리프노드까지 수를 찾는다.
public Node search(Node root, int element){
if (root==null || root.data==element) // 종료 조건 : 루트가 비어있거나 키가 루트에 없는 경우
return root;
if (root.data < element) // 찾는 원소가 루트의 데이터보다 클 경우
return search(root.right, element);
return search(root.left, element); // 찾는 원소가 루트의 데이터보다 작을 경우
}
(2) 원소 삽입 : BST에 특정 원소를 삽입함(추가)

❶ 가장 첫번째로 삽입하는 원소라면(BST empty) root 노드로 지칭
❷ 그 다음 원소를 삽입할 때, root 노드보다 작으면 왼쪽 트리, 크면 오른쪽 트리로 포인터를 연결해 추가
❸ 기존 BST 에 새로운 원소를 삽입한다면 search를 통해 자리를 찾아 추가
class BinarySearchTree {
void insert(int element) { root = insertRec(root, element); } // 삽입 메서드
Node insertRec(Node root, int element){
if (root == null) { // 트리가 비어있거나 비어있는 루트 노르를 찾았다면 새로운 노드를 루트로 만들고 반환
root = new Node(element);
return root;
}
else if (element < root.data) // 그렇지 않으면 데이터를 비교하며 트리 재귀 탐색
root.left = insertRec(root.left, element);
else if (element > root.data)
root.right = insertRec(root.right, element);
return root;
}
public static void main(String[] args){
BinarySearchTree tree = new BinarySearchTree();
/* 생성할 BST 트리
50
/ \
30 70
/ \ / \
20 40 60 80 */
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
}
}
(3) 원소 삭제: 특정 원소를 BST에서 삭제
: 3가지 경우
① 자식이 없는 노드를 삭제할 경우(리프 노드)
② 자식이 하나 있는 노드를 삭제할 경우
③ 자식이 두개 있는 노드를 삭제할 경우
① 자식이 없는 노드를 삭제할 경우(리프 노드) : 찾아서 삭제하면 됨
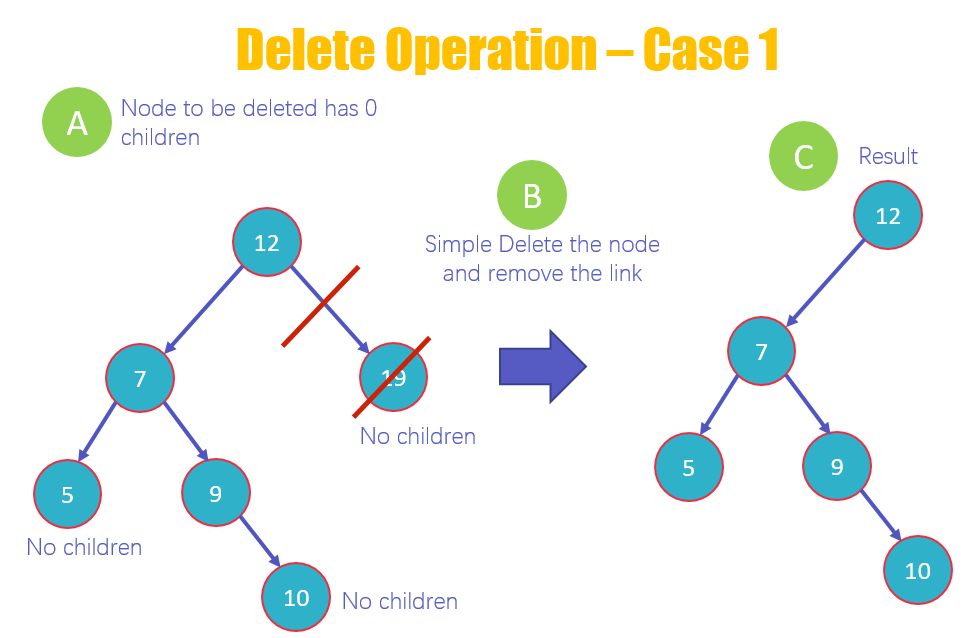
② 자식이 하나 있는 노드를 삭제할 경우 : 찾아서 삭제하고 자식 노드를 본인 자리에 넣어주면 됨

③ 자식이 두개 있는 노드를 삭제할 경우 : 찾아서 삭제하고 해당 노드를 기준으로
(a) 왼쪽 트리의 가장 오른쪽에 있는 노드를 해당 노드 자리로 옮겨주거나
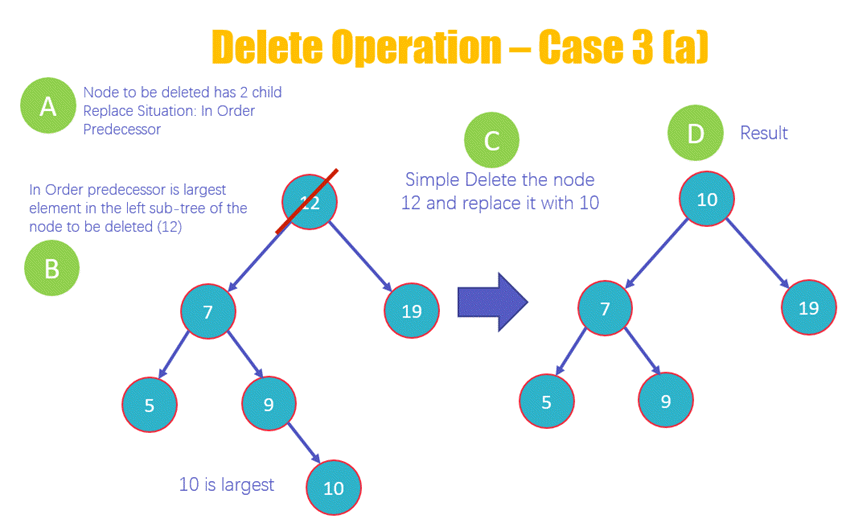
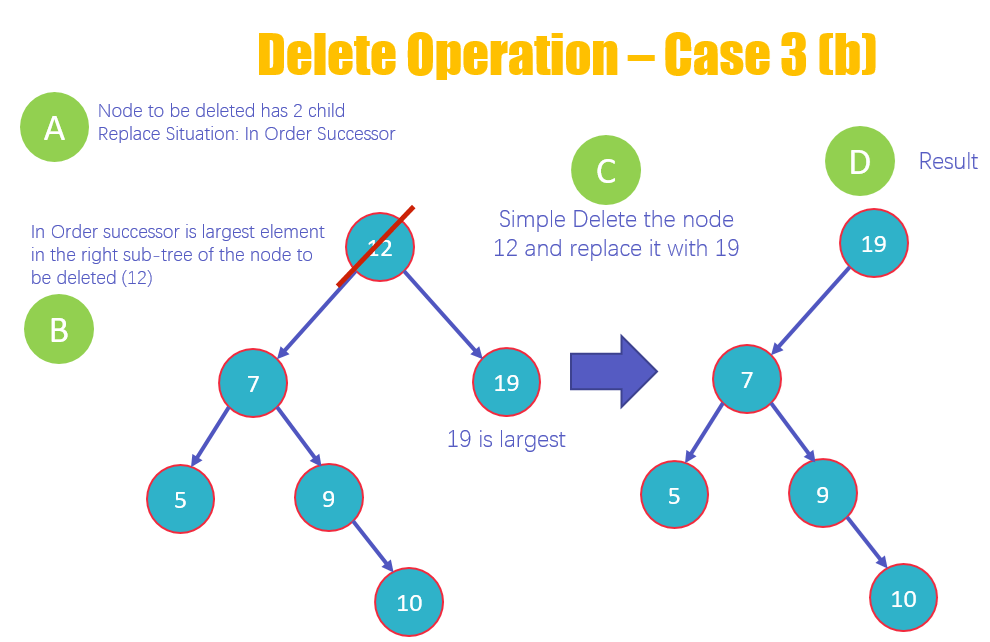
(b) 오른쪽 트리의 가장 왼쪽에 있는 노드를 해당 자리로 옮겨줌
class BinarySearchTree {
void deleteKey(int element) { root = deleteRec(root, key); } // 삭제 메서드
Node deleteRec(Node root, int element)
{
if (root == null) // 종료 조건 : 루트 노드가 비어있을 경우(못 찾음) 루트 반환
return root;
if (element < root.data) // 루트 데이터보다 작으면 왼쪽 트리 탐색
root.left = deleteRec(root.left, element);
else if (element > root.data) // 루트 데이터보다 크면 오른쪽 트리 탐색
root.right = deleteRec(root.right, element);
else { // 같으면, 원소를 찾았으므로 삭제
// 1, 2경우 (없거나 자식 하나) : 삭제의 의미는 null로 만들어주기
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// 3-(b)의 경우, 오른쪽 트리에서 가장 작은 값(가장 왼쪽 위치)을 찾아서 루트 데이터에 넣어줌
root.data = minValue(root.right);
// 루트에 넣어준 데이터를 트리에서 찾아서 삭제해줌
root.right = deleteRec(root.right, root.data);
}
return root;
}
int minValue(Node root) { // 최솟값을 찾는 메서드
int minv = root.data;
while (root.left != null) { // 왼쪽 트리가 비어있을 때까지 내려가서 찾아줌
minv = root.left.data;
root = root.left;
}
return minv;
}
}
🙋 이진탐색트리의 편향성을 개선하기 위한 방법?
🧲 출처
https://www.guru99.com/binary-search-tree-data-structure.html
Binary Search Tree (BST) with Example
What is a Binary Search Tree? The binary search tree is an advanced algorithm used for analyzing the node, its left and right branches, which are modeled in a tree structure and returning the value.
www.guru99.com