[CS 스터디: JAVA] (8) 거품 정렬, 선택 정렬, 삽입 정렬
정렬 : 순서 없이 배열된 있는 자료들을 그 값에 따라 순서에 따라 재배열하는 것
| 오름차순 정렬 (Ascending, 작은 → 큰) | 내림차순 정렬 (Descending, 큰 → 작은) | |
| 숫자 | 1 2 3 4 ... | 10 9 8 7 ... |
| 영어 | a b c ... z (알파벳 순) | z y x ... a (알파벳 역순) |
| 한글 | ㄱ ㄴ ㄷ ... ㅎ | ㅎ ㅍ ㅌ ... ㄱ |

거품 정렬(Bubble Sort)
: 가장 단순하고 직관적인 정렬 알고리즘
: 간단한 코드가 필요할 때에나 복잡도가 중요하지 않은 문제에서 사용
: 인접한 두 원소를 비교(Compare)해 조건에 맞지 않다면 두 원소를 바꿔줌 (Swap)
: Compare and Swap Cycle
✓ 1번째 순회 (Step 0)
① 배열의 첫번째 인덱스(i = 0)부터 시작한다.
② 해당 인덱스(i)와 다음 인덱스(i+1)를 비교해 조건에 맞지 않으면(오름차순 정렬 시, arr[i] > arr[i+1] 일 경우) 바꿔준다.
③ (i+1) 이 마지막 인덱스가 될 때까지 ②를 수행한다.
✅ 순회를 끝낸 배열의 가장 마지막 원소는 배열의 최댓값이 오게된다. (계속해서 큰 수는 바꿔주었기 때문에 맨 뒤로 밀림)
✓ 나머지 순회 (Step 1, 2..)
위의 방법 (i+1)을 1씩 줄이면서(✅의 내용 때문에) 반복한다.
✓ 마지막 순회 (Step N-2)
(i+1)이 1이 될 때 순회가 종료된다. 총 N-2(=N-1-1)번 순회가 이루어짐을 확인할 수 있다.

구현 코드
static void bubbleSort(int array[]) {
int size = array.length;
for (int i = 0; i < size - 1; i++)
for (int j = 0; j < size - i - 1; j++){ // 맨 마지막 원소의 인덱스에 주목
if (array[j] > array[j + 1]) { // 인접한 원소 Compare, 오름차순이 아닐 경우 Swap
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
거품정렬은 만약 [0, 1, 2, 3, 6, 5] 의 배열이 들어왔을 때 어떻게 작동할까
위의 코드대로라면 똑같이 N - 2번 수행하며 불필요한 연산을 진행하게 된다. 사실상 Step 0 에서 6과 5를 바꾸면 끝나는 문제지만 말이다. 이것을 해결하기 위해서(이미 정렬된 배열에 대해서도 계속해서 정렬 진행) 거품정렬 최적화를 진행해야 한다.
최적화를 위해 swapped 라는 변수를 추가로 사용한다. 만약 step 도중 swap이 일어나면 swapped = true 가 된다. 그렇지 않으면 swapped = false 이다. 만약에 반복문을 순회하다 swapped = false로 남아있을 경우, 더 이상 swap을 진행하지 않아도 되므로 후의 순회가 필요 없다는 뜻이다.
static void bubbleSort(int array[]) {
int size = array.length;
for (int i = 0; i < size - 1; i++)
boolean swapped = false; // swapped 변수 도입
for (int j = 0; j < size - i - 1; j++){ // 맨 마지막 원소의 인덱스에 주목
if (array[j] > array[j + 1]) { // 인접한 원소 Compare, 오름차순이 아닐 경우 Swap
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
swapped = true; // swap이 일어났을 경우 값 변경
}
}
if(!swapped){ // swap이 일어나지 않았을 경우 이미 정렬된 배열이라는 의미
break;
}
}
복잡도
✅ 시간복잡도
거품 정렬의 기본 수행 횟수는 Step 0(n-1 번 비교) + Step1 (n-2번 비교) + ... + Step 마지막(1번 비교) 이므로 아래와 같이 된다.
(n-1) + (n-2) + (n-3) +.....+ 1 = n(n-1)/2
→ (n²) 번의 시간 복잡도
최악과 평균 시간 복잡도 : O(n²) → 모두 다 정렬을 해봐야 하는 경우
최고 평균 시간 복잡도 : O(n) → 이미 정렬되어 있는 배열에서는 swapped만 확인하고 정렬할 필요 x
✅ 공간복잡도
O(1) → tmp를 제외하고는 여분의 배열 공간이 필요하지 않음, 만약 swapped도 사용하면 O(2)가 됨
선택 정렬(Selection Sort)
: 정렬되지 않은 배열에서 최솟값을 선택해 정렬되지 않은 배열의 첫번째 인덱스에 넣어주는 알고리즘
: 크기가 작은 리스트를 정렬할 때, 모든 원소를 확인해야만 할 때 사용
: 거품정렬에 비해 Swap(Replace) 횟수가 적음 → 거품 정렬보다 아주 조금 더 빠르다
: Select and Replace Cycle
✓ 1번째 순회 (Step 1)
① 가장 첫번째 원소를 최솟값으로 선택(min = arr[0])한다.
② 최솟값과 i번째 원소를 비교해 i번째 원소가 더 작을 경우, 최솟값을 교체한다.
③ i 가 (N-1)이 될 때까지 ②를 반복해 배열의 최솟값을 찾는다.
④ min과 첫번째 원소를 바꿔준다.
✅ 순회를 끝낸 배열의 가장 첫번째 원소는 배열의 최솟값이 오게된다. 두번째부터 마지막 인덱스까지의 배열은 정렬되지 않은 상태로 남는다.
✓ 나머지 순회 (Step 2, 3..)
배열 순회의 시작을 i 번째부터로 바꾸고 위의 과정을 반복한다.

코드 구현
void selectionSort(int array[]) {
int size = array.length;
for (int step = 0; step < size - 1; step++) {
int min_idx = step; // 교환을 하기 위한 인덱스를 첫 인덱스로 지정
for (int i = step + 1; i < size; i++) {
if (array[i] < array[min_idx]) { // 값 비교 후 더 작은 값이 나오면 인덱스 변경
min_idx = i;
}
}
int temp = array[step]; // 첫번째 원소와 최솟값 교체
array[step] = array[min_idx];
array[min_idx] = temp;
}
}
거품정렬과는 다르게 배열이 이미 다 정렬이 되어 있다고 해도 확인할 방법이 없다. 최적화 실패!
복잡도
✅ 시간 복잡도
(n-1) + (n-2) + (n-3) +.....+ 1 = n(n-1)/2
→ (n²) 번의 시간 복잡도
최악, 평균, 최선의 시간 복잡도 : O(n²)
✅ 공간 복잡도
temp 사용으로 O(1)
삽입 정렬(Insertion Sort)
: 선택 정렬과 유사하지만 조금 더 효율적인 알고리즘
: 2번째 원소부터 시작해 더 작은 인덱스의 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입하는 알고리즘
① 가장 첫번째 원소가 정렬되어 있다고 가정하고 두번째 원소를 key에 저장한다.
② key를 첫번째 원소와 비교해 만약 key가 작을 경우 key는 첫번째 원소의 앞으로 위치해준다.
✅ 첫번째, 두번째 원소는 정렬됨
③ 세 번째 원소를 key에 저장하고 왼쪽 배열과 비교해 자리를 찾아준다.
✅ 세번째 원소까지 정렬됨
④ i 번째 원소를 key에 저장하고 왼쪽 배열과 비교해 자리를 찾아준다.
✅ i 번째 원소까지 정렬됨
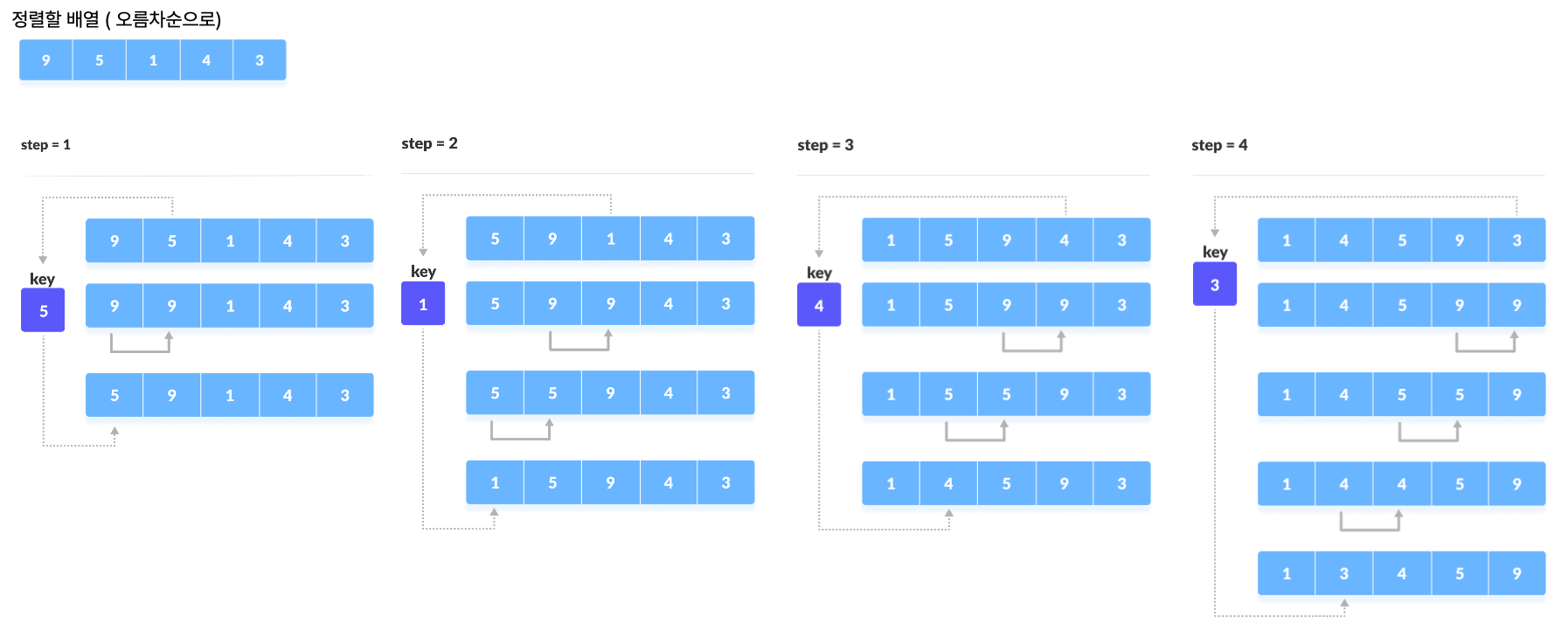
구현 코드
void insertionSort(int array[]) {
int size = array.length;
for (int step = 1; step < size; step++) { // 두번째 원소부터 시작
int key = array[step]; // 키에 저장
int j = step - 1; // step 원소 기준 왼쪽을 순회
while (j >= 0 && key < array[j]) { // 비교 후 위치 변경
array[j + 1] = array[j];
--j;
}
array[j + 1] = key; // 찾은 위치에 삽입
}
}
복잡도
✅ 시간 복잡도
최악의 경우 : O(n²) (n*(n-1))→ 내림차순을 오름차순으로 정렬하고 싶을 경우, 모든 i 번째 원소가 key가 될 때 i-1 번의 비교가 필요
최선의 경우 : O(n) → 이미 정렬된 배열일 경우
평균 : O(n²)
✅ 공간 복잡도
key 사용으로 O(1)