👇🏻 오늘도 지나칠 수 없는 오늘의 짤

저번 포스트에서 공부했던 이진 트리의 응용버전(?)을 공부하도록 하겠다.
✅ 이진 탐색 트리란
이진 탐색 트리(Binary Search Tree)는 주로 BST라고 부르고 쉽게 말해 [이진 트리 + 조건 한 개 추가]를 만족하는 자료형이다.
바로 그 조건은 듣기에는 간단하다.
-> (모든 노드에 대해) 왼쪽 노드.data < 오른쪽 노드.data
이진 탐색 트리(Binary Search Tree, BST) : 모든 노드에 대해 왼쪽 노드의 데이터가 오른쪽 노드의 데이터보다 작음을 만족하는 이진 트리
이진 탐색 트리의 조건은 그다지 까다롭게 느껴지지는 않지만 막상 구현해 보면 생각보다 어렵다고 느끼게 될 것이다.
왜냐하면 트리에 데이터를 삽입하고 삭제할 때, 조건을 만족시키기 위해 트리를 다시 정렬해야 하는 경우가 빈번히 생기기 때문이다.
노드와 이진 탐색 트리를 찍어내는 틀은 이전 포스트와 동일하다.
class Node:
def __init__(self, data, left = None, right = None):
self.data = data
self.left = left
self.right = right
class BinarySearchTree():
def __init(self):
self.root = None
✅ 이진 탐색 트리 데이터 삽입
이진 탐색 트리에 새로운 데이터를 삽입해보자. 단, 값이 중복되는 노드는 삽입하지 않기로 한다.
알고리즘은 다음과 같다.
1. root가 None일 경우에는, root에 삽입
2. root가 존재할 경우에는, 값을 비교해서 삽입
1. 현재 root에 있는 값이 중심이 되는 값이므로 node=root에서 시작한다.
[while 반복문]
2. node.data보다 새로운 데이터 값이 작을 경우, node를 왼쪽 트리로 이동시킴.
어느 순간, 새로운 데이터 값이 작지 않을 경우, node.left에 새로운 데이터를 넣어주면 된다.
3. node.data보다 새로운 데이터 값이 클 경우, node를 오른쪽 트리로 이동시킴.
어느 순간, 새로운 데이터 값이 크지 않을 경우, node.right에 새로운 데이터를 넣어주면 된다.
class BinarySearchTree():
def __init__(self):
self.root = None
def insert(self, new_data):
if self.root == None:
self.root = Node(new_data)
else:
node = self.root
while True:
if new_data < node.data:
if node.left != None:
node = node.left
else:
node.left = Node(new_data)
break
else:
if node.right != None:
node = node.right
else:
node.right = Node(new_data)
break
다음과 같이 구현하고 아무 생각없이 1에서 9까지의 데이터를 삽입하고 전위 순회로 출력해봤더니 계속 1 2 3 4 5 6 7 8 9 가 나왔다.


내가 생각한대로라면 6 4 2 1 3 5 8 7 9 가 나와야 하는데...이러면서 뭐지 했는데 우리가 짠 코드는 완전이진탐색트리가 아니었기 때문에 오른쪽과 같은 그림으로 삽입이 되고 있었던 것이었다. 하하. 뭐지 바보인가 하는 생각해도 인정...
그래서 아마 데이터를
BST.insert(6)
BST.insert(4)
BST.insert(1)
BST.insert(7)
BST.insert(9)
BST.insert(23)
BST.insert(46)
BST.insert(3)
BST.insert(11)✅ 이진 탐색 트리 데이터 삭제
이제 삭제에 대해 알아보아야 하는데 삭제하려는 노드가 몇 명의 자식을 얼마나 가지고 있냐에 따라 다르기 때문에 경우의 수를 나누어 생각해야 한다. 경우의 수를 전부 다 찾아내기 쉽게 조금 복잡하게 생긴 트리로 생각해보자.

1. 자식이 없는, 리프 노드를 삭제할 경우
2. 자식이 하나인 노드를 삭제할 경우
3. 자식이 둘인 노드를 삭제할 경우
일단, 삭제를 하기 이전에 해야 할 것은 삭제하려는 노드를 찾는 것이다. 삽입과 같은 방법으로 찾아주면 된다.
단, 찾으려는 노드 뿐만 아니라 삭제를 쉽게 하기 위해 해당 노드의 부모 노드도 함께 찾는다.
찾는 노드가 있을 경우는 (node, node의 head), 없을 경우는 None을 반환한다.
def findNode(self, findValue):
node = self.root
while node:
if node.data == findValue:
return (node, self.parent)
else:
if node.data > findValue:
self.parent = node
node = node.left
else:
self.parent = node
node = node.right
return None
1. 자식이 없는, 리프 노드를 삭제할 경우

이 경우는 매우 간단하다.
1. 노드가 자식이 있는지 확인
2. 노드가 부모 노드의 왼쪽 자식인지, 오른쪽 자식인지 확인을 한 후, 자식의 연을 끊기(None).
def delete(self,deleteData):
deleteNode, deleteParentNode = self.findNode(deleteData)
# 삭제할 노드에 자식이 없을 때
if deleteNode.left == None and deleteNode.right == None:
# 삭제할 노드가 부모 노드에게 왼쪽 자식일 때
if deleteData < deleteParentNode.data:
deleteParentNode.left = None
# 삭제할 노드가 부모 노드에게 오른쪽 자식일 때
else:
deleteParentNode.right = None
2. 자식이 하나인 노드를 삭제할 경우


예를 들어 9를 삭제하려고 할 때, 9의 왼쪽 자식 노드인 8이 9의 자리에 가면 된다.
1. 삭제할 노드에게 왼쪽 자식이 있는지, 오른쪽 자식이 있는지 판별
2. 노드가 부모 노드의 왼쪽 자식인지, 오른쪽 자식인지 판별
3. 부모 노드에게 삭제할 노드의 자식을 연결
# 삭제할 노드에 왼쪽 자식이 있을 때
elif deleteNode.left != None and deleteNode.right == None:
# 삭제할 노드가 부모 노드에게 왼쪽 자식일 때
if deleteData < deleteParentNode.data:
deleteParentNode.left = deleteNode.left
# 삭제할 노드가 부모 노드에게 오른쪽 자식일 때
else:
deleteParentNode.right = deleteNode.left
# 삭제할 노드에 오른쪽 자식이 있을 때
elif deleteNode.left == None and deleteNode.right != None:
# 삭제할 노드가 부모 노드에게 왼쪽 자식일 때
if deleteData < deleteParentNode.data:
deleteParentNode.left = deleteNode.right
# 삭제할 노드가 부모 노드에게 오른쪽 자식일 때
else:
deleteParentNode.right = deleteNode.right
2. 자식이 둘인 노드를 삭제할 경우

위의 그림에서 4를 삭제해보자. 4를 삭제하려면 4의 자리에 누군가가 와야 한다.
그 누군가는 삭제할 노드의 왼쪽 트리 중 가장 큰 수(왼쪽 트리에서 가장 오른쪽에 위치)가 오거나
삭제할 노드의 오른쪽 트리 중 가장 작은 수(오른쪽 트리에서 가장 왼쪽에 위치)가 오면 된다.

둘 중 어떠한 반식으로 해도 이진 탐색 트리의 조건을 만족한다.
1. 삭제할 노드의 왼쪽 트리 중 가장 큰 수(가장 오른쪽에 있는 수)로 대체할 경우
1. 삭제할 노드의 왼쪽 트리에서 가장 오른쪽에 있는 노드를 찾고, 해당 노드의 부모 노드의 오른쪽 자식을 None으로 설정한다.
2. 삭제할 노드가 부모 노드의 왼쪽 자식인 경우, 부모 노드의 왼쪽 자식을 가장 오른쪽에 있는 노드와 연결을 한다.
3. 가장 오른쪽에 있는 노드의 오른쪽 자식을 삭제 노드의 오른쪽 자식과 연결, 왼쪽 자식은 삭제 노드의 왼쪽 자식과 연결
2. 삭제할 노드의 오른쪽 트리 중 가장 작은 수(가장 왼쪽에 있는 수)로 대체할 경우
1. 삭제할 노드의 오른쪽 트리에서 가장 왼쪽에 있는 노드를 찾고, 해당 노드의 부모 노드의 왼쪽 자식을 None으로 설정한다.
2. 삭제할 노드가 부모 노드의 오른쪽 자식인 경우, 부모 노드의 으론쪽 자식을 가장 왼쪽에 있는 노드와 연결을 한다.
3. 가장 왼쪽에 있는 노드의 왼쪽 자식을 삭제 노드의 왼쪽 자식과 연결, 오른쪽 자식은 삭제 노드의 오른쪽 자식과 연결
나는 1번 방법으로 구현할 것이다. 근데 하자마자 발견한...
🤬 에러 1
# 왼쪽 트리의 가장 오른쪽 노드를 찾는 함수
# 해당 노드와 해당 노드의 부모 노드를 반환한다
def findMostRightNode(self, node):
while node.right:
self.parent = node
node = node.right
return (node, self.parent)
# 구현 코드
else:
MostRightNode, MostRightNodeParent = self.findMostRightNode(deleteNode.left)
MostRightNodeParent.right = None
deleteParentNode.left = MostRightNode
MostRightNode.left = deleteNode.left
MostRightNode.right = deleteNode.right
내가 테스트코드로 해 본 것은 루트 노드를 삭제하는 것이었다. 근데 루트 노드는 부모 노드가 없어서 부모 노드가 None으로 반환되는 바람에 루트 노드에 대한 예외처리를 따로 해 주었다.
def delete(self,deleteData):
# 루트 노드를 삭제할 경우
if self.root.data == deleteData:
# 삭제할 루트 노드가 오른쪽 자식만 있는 경우
if self.root.left != None and self.root.right == None:
self.root = self.root.left
# 삭제할 루트 노드가 왼쪽 자식만 있는 경우
elif self.root.left == None and self.root.left != None:
self.root = self.root.right
# 삭제할 루트 노드가 오른쪽, 왼쪽 자식이 모두 있는 경우
else:
MostRightNode, MostRightNodeParent = self.findMostRightNode(self.root.left)
MostRightNodeParent.right = None
temp = self.root
self.root = MostRightNode
MostRightNode.left = temp.left
MostRightNode.right = temp.right
else:
# 루트 노드를 삭제하지 않을 경우
🤬 에러 2
이것을 해결하고 나서 룰루랄라 다른 노드를 삭제하는 것으로 코드를 돌려보니 또 에러가 났다.

위와 같은 경우에서 [4를 삭제 -> 2로 대체] 하는 것인데 4의 왼쪽 트리의 가장 큰 값을 찾는 findMostRightNode함수에서 왼쪽 트리에 자식 노드가 1개밖에 없을 경우 while 반복문을 한번밖에 돌지 않기 때문에, 삭제하는 노드의 부모노드(7)과 가장 오른쪽에 있는 노드의 부모노드(7)의 값이 같아 알고리즘대로 짰을 때에 삭제할 부모의 오른쪽 자식(10)이 None이 되어 버린다.
그래서 결국 이 예외도 추가해주었다.
else:
MostRightNode, MostRightNodeParent = self.findMostRightNode(deleteNode.left)
# 예외 처리문
if MostRightNodeParent.data == deleteParentNode.data:
if deleteData < deleteParentNode.data:
deleteParentNode.left = MostRightNode
MostRightNode.right = deleteNode.right
else:
deleteParentNode.right = MostRightNode
MostRightNode.right = deleteNode.right
else:
MostRightNodeParent.right = None
deleteParentNode.left = MostRightNode
MostRightNode.left = deleteNode.left
MostRightNode.right = deleteNode.right
🤬 에러 3
여기서 끝인 줄 알았건만.. 또 에러가 나는 경우가 있었다.
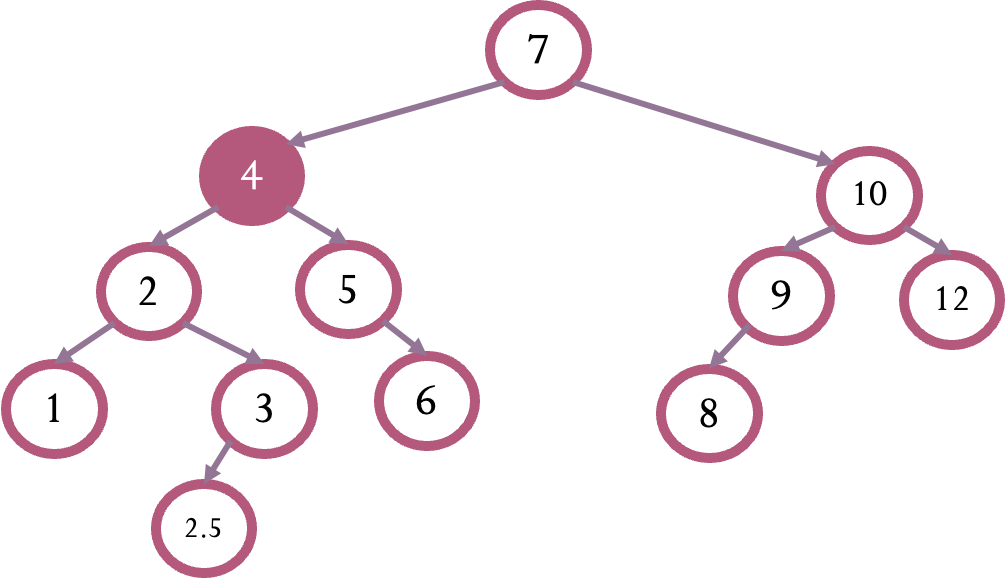
여기서 삭제할 경우, 4 -> 3(4의 오른쪽 트리에서 가장 큰 값)으로 바뀌지만 3에게 있는 2.5 자식을 처리해주지 않으면 쥐도새도 모르게 사라진다. 그래서 왼쪽 자식이 있을 경우(오른쪽 자식이 있다면 걔가 MostRightNode였겠지..)에 대해 처리해주었더니 되었다..하하
else:
MostRightNode, MostRightNodeParent = self.findMostRightNode(deleteNode.left)
if MostRightNodeParent.data == deleteParentNode.data:
if deleteData < deleteParentNode.data:
deleteParentNode.left = MostRightNode
MostRightNode.right = deleteNode.right
else:
deleteParentNode.right = MostRightNode
MostRightNode.right = deleteNode.right
else:
# 왼쪽 자식이 있을 경우
if MostRightNode.left != None:
MostRightNodeParent.right = MostRightNode.left
# 자식이 없을 경우
else:
MostRightNodeParent.right = None
deleteParentNode.left = MostRightNode
MostRightNode.left = deleteNode.left
MostRightNode.right = deleteNode.right
근데 나 아무래도 코드 너무 조잡하게 짠 거 같은데... 이게 맞나 싶다...
다른 블로그들과 책들을 참고해서 다시 짜보도록...하겠다...
👇🏻 최종 코드는 아래 Git 확인해주셈..
https://github.com/Seeun-Lim/Data-Structure/blob/main/BinarySearchTree.py
GitHub - Seeun-Lim/Data-Structure
Contribute to Seeun-Lim/Data-Structure development by creating an account on GitHub.
github.com
'Python > [Data Structure] 자료구조' 카테고리의 다른 글
| [10] Hash Table, 해시 테이블 (0) | 2022.04.21 |
|---|---|
| [9] Priority Queue, 우선순위 큐 & Heap, 힙 (0) | 2022.04.20 |
| [7] Tree, 트리 (0) | 2022.04.18 |
| [6] Queue, 큐 (0) | 2022.04.13 |
| [5] Stack, 스택 (0) | 2022.04.13 |
