DP의 핵심
Memoization : 메모이제이션 (top, down)
Tabulation : 타뷰레이션(bottom up)
Alvin's Memoization Recipe
1. Make it work
- visualize the problem as a tree
- implement the tree using recursion
- test
2. Make it efficient
- add a memo object (set,arr,..)
- add a base case to return memo values
- store return values into the memo
피보나치
❌ DP
def fibonacci(n):
if n <= 2:
return 1
return fibonacci(n-1)+fibonacci(n-2)
✅ DP
def fibonacci(n, memo):
if n in memo: return memo[n]
if n <= 2: return 1
memo[n] = fibonacci(n-1, memo) + fibonacci(n-2, memo)
return memo[n]
DP로 푸는 이유는 시간, 공간 복잡도와 연관이 있다.


Memoized 없이 푼다면 재귀 트리는 왼쪽과 같이 된다. 호출하는 n의 모든 재귀값(파란 지점)을 방문해야 한다. 이 때의 시간 복잡도는 O(2^n)이 된다.
반면에 Memoized하여 푼다면(오른쪽), 방문하는 파란 지점이 확연히 줄어든 것을 볼 수 있다. 이 때의 시간, 공간 복잡도는 O(n)이 된다.
만약, n=50 이라고 가정해보자.
Memoized ❌ : 2^50 steps => 1,125,899,906,842,624 steps
Memoized ✅ : 50 steps
확연한 차이가 난다.
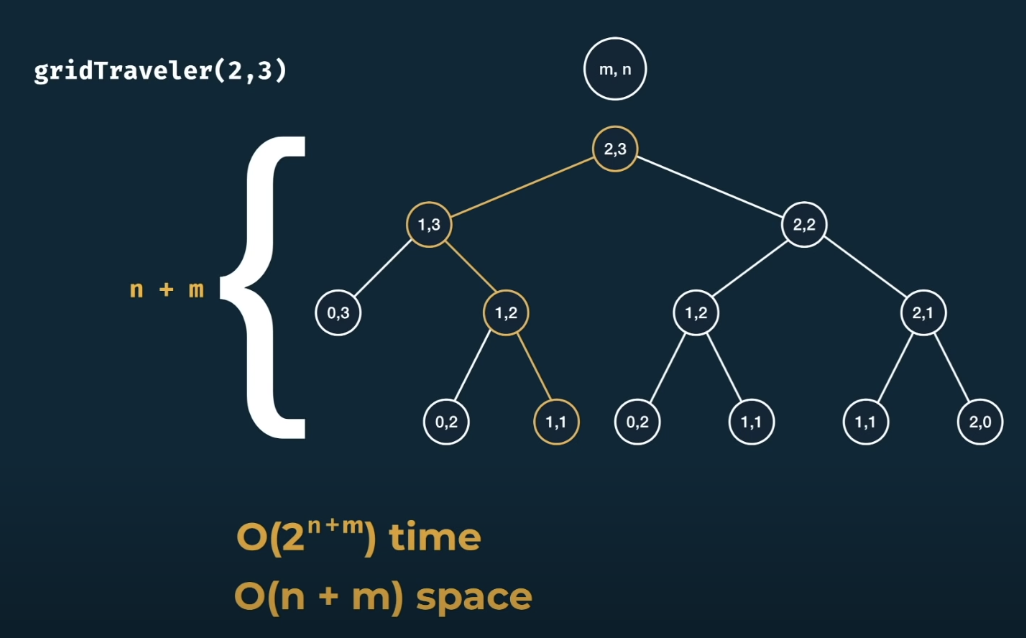
gridTraveler(m,n)
mXn의 배열의 (1,1)에서 (m,n)까지 가는 경우의 수
❌ DP , brute force [시간 복잡도 : O(2^(n+m)), 공간 복잡도 : O(n+m)]
def gridTraveler(m,n):
if m==0 or n==0: return 0
if m==1 and n==1: return 1
return gridTraveler(m-1,n)+gridTraveler(m,n-1)
✅ DP [시간 복잡도 : O(m*n), 공간 복잡도 : O(n+m)]
def gridTraveler(m,n,memo):
if (m,n) in memo: return memo[(m,n)]
if m == 0 or n == 0: return 0
if m == 1 and n == 1: return 1
memo[(m,n)] = gridTraveler(m-1, n, memo) + gridTraveler(m, n-1, memo)
return memo[(m,n)]
gridTraveler(18,18)의 값을 돌려보면 ❌ DP는 시간 초과가 되고 ✅ DP는 제대로 작동한다.
canSum(targetSum, numbers) : Decision Problem
numbers 배열에 있는 원소들을 가지고 targetSum을 만들 수 있으면 true, 그렇지 않으면 false를 반환하는 함수
ex) canSum(7, [5,3,4,7]) 👉🏻 true, canSum(7, [2,4]) 👉🏻 false
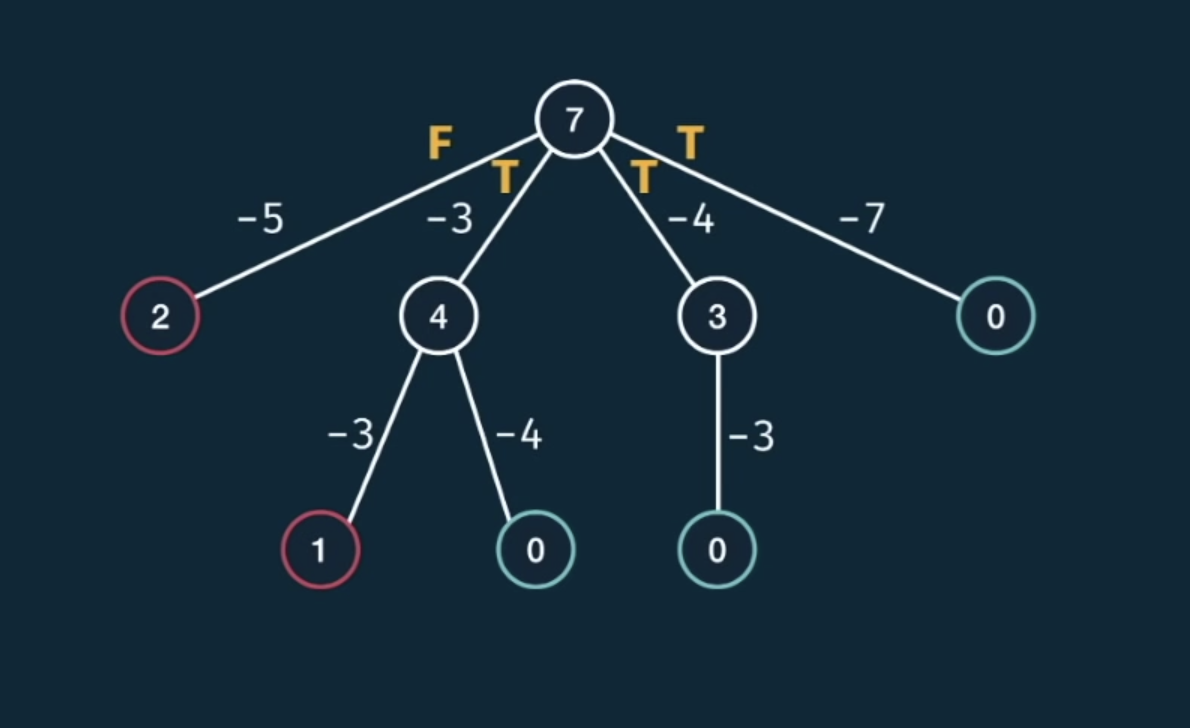
하나라도 True일 경우, True로 인식(가능은 하니깐)
m: target sum, n: numbers length
❌ DP, brute force : [시간복잡도 : O(n^m), 공간복잡도 : O(m)]
def canSum(targetSum, numbers):
if targetSum == 0: return True
if targetSum < 0: return False
for num in numbers:
if canSum(targetSum-num, numbers):
return True
return False
✅ DP : [시간복잡도 : O(n*m), 공간복잡도 : O(m)]
def canSum(targetSum, numbers, memo):
if targetSum in memo: return memo[targetSum]
if targetSum == 0: return True
if targetSum < 0: return False
for num in numbers:
if canSum(targetSum-num, numbers, memo):
memo[targetSum] = True
return True
memo[targetSum] = False
return False
howSum(targetSum, numbers) : Combinatoric Problem
numbers의 원소로 targetSum이 조합 가능한 배열을 반환함, 없으면 null 반환
ex) howSum(7, [2, 3]) 👉🏻 [3, 2, 2]
m: target sum, n: numbers length
✅ DP : [시간복잡도 : O(n*m^2), 공간복잡도 : O(m^2)]
def howSum(targetSum, numbers, memo):
if targetSum in memo: return memo[targetSum]
if targetSum == 0: return []
if targetSum < 0: return None
for num in numbers:
result = howSum(targetSum-num, numbers, memo)
if result is not None:
result.append(num)
memo[targetSum] = result
return memo[targetSum]
return None
bestSum(targetSum, numbers) : Optimization Problem
howSum의 값으로 나올 수 있는 배열 중, 가장 짧은 배열을 반환한다.
ex) bestSum(8, [2, 3, 5]) 👉🏻 [3, 5] (가능한 배열 : [2, 2, 2, 2], [2, 3, 3], [3, 5])
✅ DP [시간복잡도 : O(n*m^2) , 공간복잡도 : O(m^2)]
def bestSum(targetSum, numbers, memo = {}):
if targetSum in memo: return memo[targetSum]
if targetSum == 0: return []
if targetSum < 0: return None
shortestCombi = None
for num in numbers:
result = bestSum(targetSum-num, numbers, memo)
if result is not None:
combi = result[:]+[num]
if shortestCombi is None or len(combi) < len(shortestCombi):
shortestCombi = combi
memo[targetSum] = shortestCombi
return shortestCombi
'Python > [Algorithm] 알고리즘' 카테고리의 다른 글
| [백준] 다시 풀어봐야 할 문제 모음 (0) | 2022.06.03 |
|---|---|
| [Q3:English] Kth largest element (0) | 2022.06.02 |
| [Q2:English] First and last index in sorted array (0) | 2022.06.02 |
| [Q1:Korean] Anagram, 철자 확인 (0) | 2022.06.02 |
| Binary Search, 이진 탐색 (0) | 2022.05.18 |
