🔹 출처
2022.04.26 - [Python/[Algorithm] 알고리즘] - DFS & BFS, 깊이 우선 탐색과 넓이 우선 탐색 (1)
DFS & BFS, 깊이 우선 탐색과 넓이 우선 탐색 (1)
출처 : 더보기 https://www.youtube.com/watch?v=tWVWeAqZ0WU DFS와 BFS는 그래프 자료 구조를 이용한다. 더보기 2022.04.24 - [Python/[Data Structure] 자료구조] - [11] Graph, 그래프 [11] Graph, 그래프 어쨌..
sennieworld.tistory.com
{ 경로 찾기 }
출발 노드에서 도착 노드까지 경로가 있는지 탐색 : 있으면 true, 없으면 false 반환
🔹 { 사이클, Cycle }
그래프에서 노드들이 가리키는 또는 연결된 방향에 사이클이 있을 수 있다.
이는 탐색이나 경로찾기에 중요한 역할을 한다.
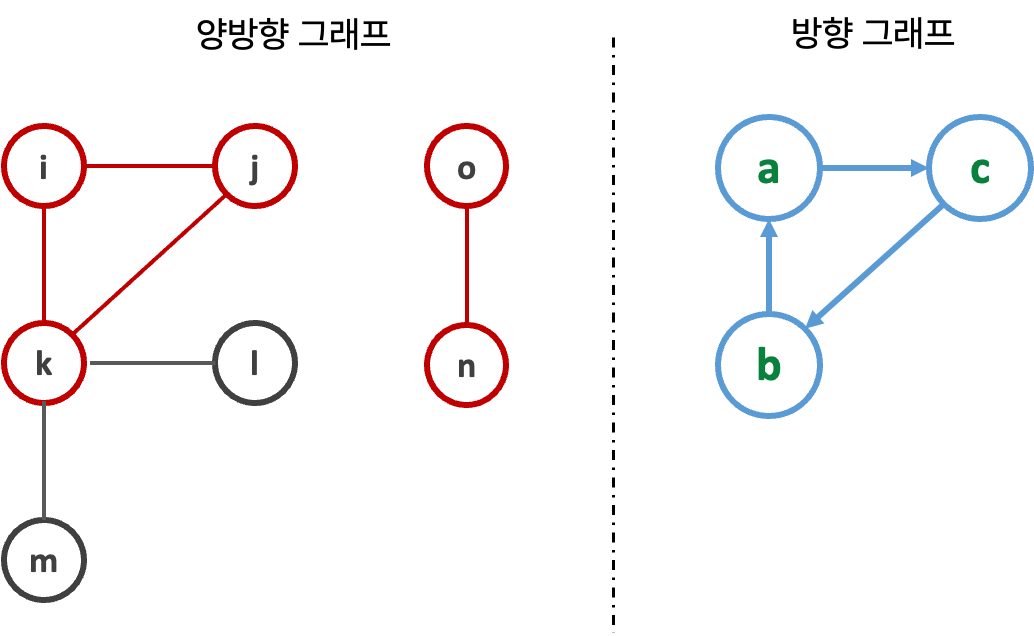
{ 방향 그래프 }
🍍 { DFS : 깊이 우선 탐색 }
1. { 그림으로 살펴보기 }
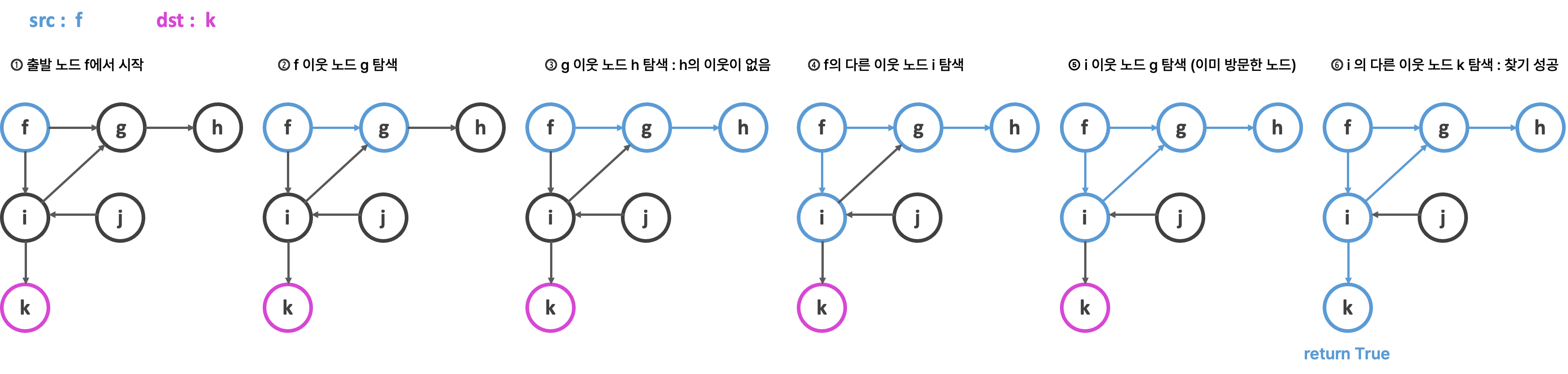
❶ 경로가 있는 경우
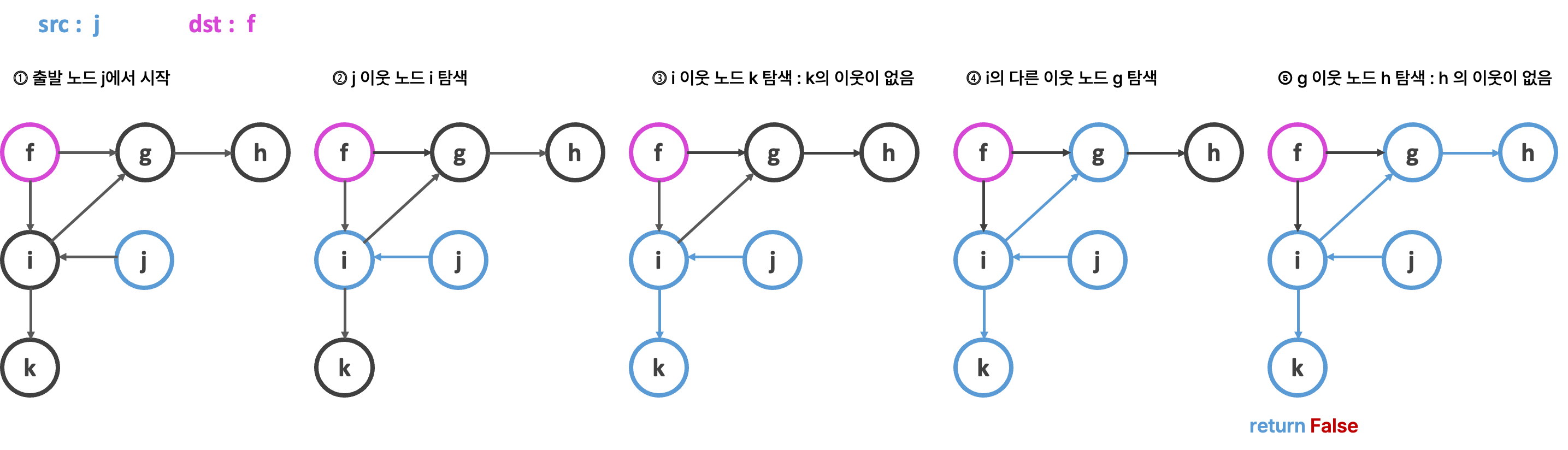
❷ 경로가 없는 경우
2. { 알고리즘 로직 }
hasPath(graph, src: 시작 노드, dst: 도착 노드):
필요한 자료구조 : stack=[], current_node
1. stack에 src를 추가한다.
[ while 반복문 : stack이 비어있지 않을 동안 ]
2. 스택의 stack.pop() 값을 pop_node에 넣어준다.
2. pop_node가 dst 값과 같으면 true를 반환한다
3. 그렇지 않으면, pop_node를 current_node로 만들어준다.
4. current_node의 이웃 노드들을 찾아 stack에 추가한다.
[ 반복문 종료 ]
5. false를 반환한다 ( dst를 못찾을 경우)
3. { 구현 }
👇🏻 알고리즘 로직을 있는 그대로 구현한 비효율적인 코드
def hasPath(graph, src, dst):
stack = []
stack.append(src)
while len(stack) != 0:
pop_node = stack.pop()
if pop_node == dst: return True
else: current_node = pop_node
for neighbor in graph[current_node]:
stack.append(neighbor)
return False
graph = {'f':[],'g':[],'h':[],'i':[],'j':[],'k':[]}
edges = [['f','g'],['f','i'],['g','h'],['i','g'],['i','k'],['j','i']]
for edge in edges:
graph[edge[0]].append(edge[1])
print(hasPath(graph, 'f','k')) # True
print(hasPath(graph, 'j','f')) # False
👇🏻 간편 코드
def hasPath(graph, src, dst):
if(src == dst):
return True
for neighbor in graph[src]:
if hasPath(graph, neighbor, dst) == True:
return True
return False
graph = {'f':[],'g':[],'h':[],'i':[],'j':[],'k':[]}
edges = [['f','g'],['f','i'],['g','h'],['i','g'],['i','k'],['j','i']]
for edge in edges:
graph[edge[0]].append(edge[1])
print(hasPath(graph, 'f','k')) # True
print(hasPath(graph, 'j','f')) # False
4. { 시간복잡도 & 공간복잡도 }
n = 노드의 개수, e = 간선의 개수
시간복잡도 O(e)
공간복잡도 O(n)
가장 최악의 경우( 간선의 개수가 노드 개수의 제곱일 때 : e = n^2) , 시간복잡도는 O(n^2)가 된다.
🎀 { BFS : 넓이 우선 탐색 }
구현 코드만 넣도록 하겠음.
from queue import Queue
def hasPath(graph, src, dst):
queue = Queue()
queue.put(src)
while not queue.empty():
current_node = queue.get()
if(current_node == dst):
return True
for neighbor in graph[current_node]:
queue.put(neighbor)
return False
graph = {'f':[],'g':[],'h':[],'i':[],'j':[],'k':[]}
edges = [['f','g'],['f','i'],['g','h'],['i','g'],['i','k'],['j','i']]
for edge in edges:
graph[edge[0]].append(edge[1])
print(hasPath(graph, 'f','k')) # True
print(hasPath(graph, 'j','f')) # False
{ 무방향 그래프 }
👇🏻 무방향 그래프 구현 코드
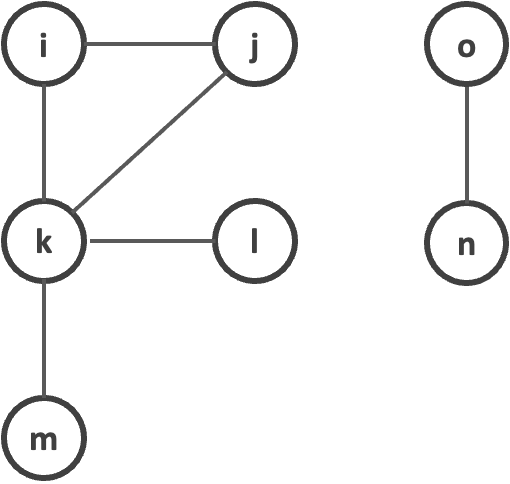
edges = [['i','j'],['k','i'],['j','k'],['m','k'],['k','l'],['o','n']]
graph = {}
for edge in edges:
if edge[0] not in graph:
graph[edge[0]] = []
if edge[1] not in graph:
graph[edge[1]] = []
graph[edge[0]].append(edge[1])
graph[edge[1]].append(edge[0])
print(graph)
# {'i': ['j', 'k'], 'j': ['i', 'k'], 'k': ['i', 'j', 'm', 'l'], 'm': ['k'], 'l': ['k'], 'o': ['n'], 'n': ['o']}
🍍 { DFS : 깊이 우선 탐색 }
1. { 그림으로 살펴보기 }
그래프에 사이클이 존재할수도 있으므로 방문한 노드를 저장하는 visited 가 필요하다. (이미 방문한 노드는 다시 방문하지 않기 위해서)
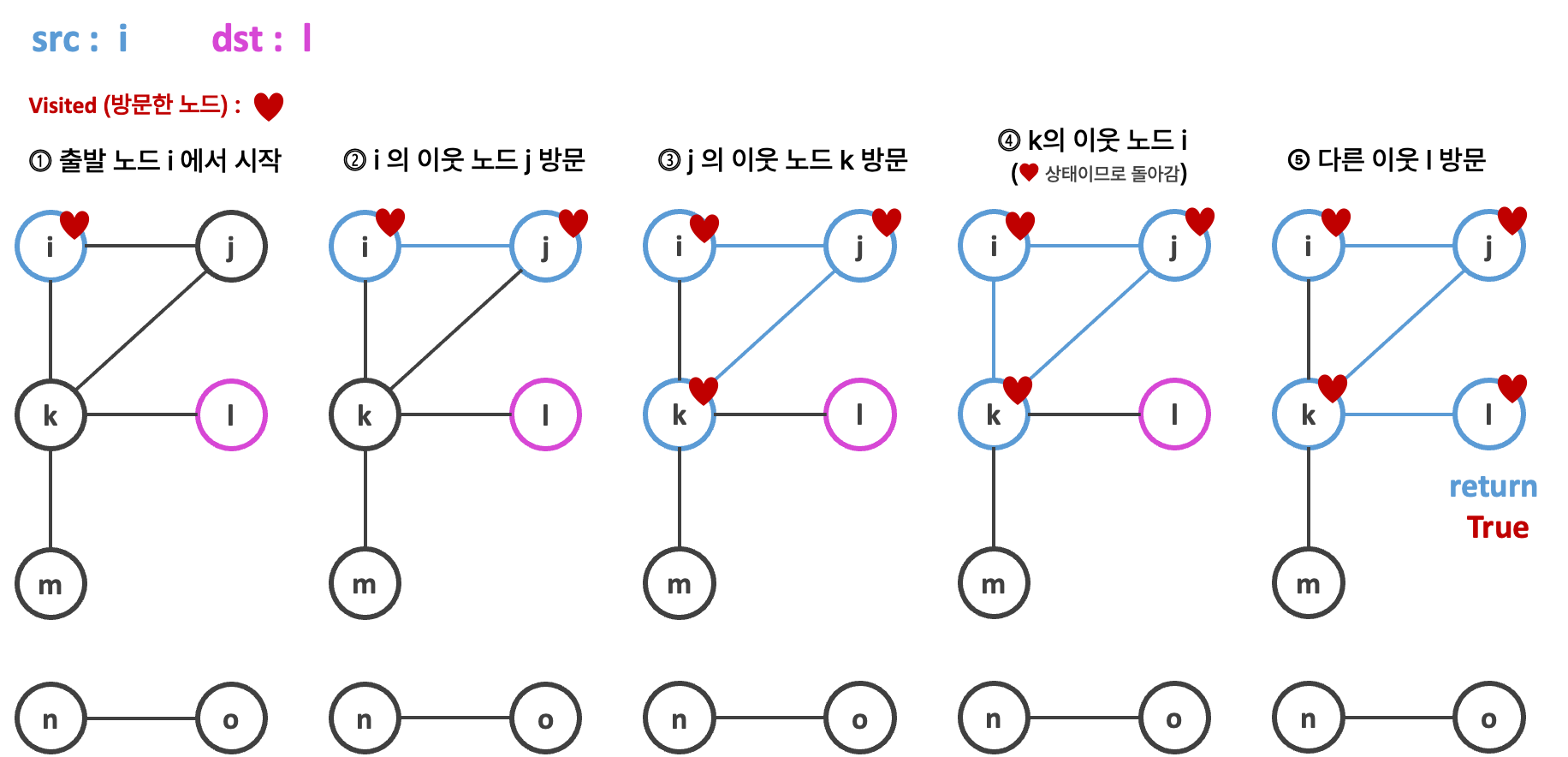
2. { 알고리즘 로직 }
hasPath(graph, src: 시작 노드, dst: 도착 노드):
필요한 자료구조 : visited = []
1. visited에 src를 추가한다.
2. 만약 src == dst가 같다면, True를 반환한다.
3. src의 이웃 노드들을 돌며 hasPath를 재귀한다.
4. 이웃 노드를 돌며 재귀하는 동안 hasPath가 True를 반환할 경우, True를 반환한다.
5. false를 반환한다 ( dst를 못찾을 경우)
3. { 구현 }
def hasPath(graph, src, dst, visited):
visited.append(src)
if src == dst: return True
for neighbor in graph[src]:
if neighbor not in visited:
if hasPath(graph, neighbor, dst, visited) == True:
return True
return False
edges = [['i','j'],['k','i'],['j','k'],['m','k'],['k','l'],['o','n']]
graph = {}
for edge in edges:
if edge[0] not in graph:
graph[edge[0]] = []
if edge[1] not in graph:
graph[edge[1]] = []
graph[edge[0]].append(edge[1])
print(hasPath(graph, 'i','l', [])) # True
print(hasPath(graph, 'i','n', [])) # False
4. { 시간복잡도 & 공간복잡도 }
n = 노드의 개수, e = 간선의 개수
시간복잡도 O(e)
공간복잡도 O(n)
가장 최악의 경우( 간선의 개수가 노드 개수의 제곱일 때 : e = n^2) , 시간복잡도는 O(n^2)가 된다.
🎀 { BFS : 넓이 우선 탐색 }
역시나 코드만!
from queue import Queue
def hasPath(graph, src, dst, visited):
queue = Queue()
queue.put(src)
while not queue.empty():
current_node = queue.get()
visited.append(current_node)
if(current_node == dst): return True
for neighbor in graph[current_node]:
if neighbor not in visited:
queue.put(neighbor)
return False
edges = [['i','j'],['k','i'],['j','k'],['m','k'],['k','l'],['o','n']]
graph = {}
for edge in edges:
if edge[0] not in graph:
graph[edge[0]] = []
if edge[1] not in graph:
graph[edge[1]] = []
graph[edge[0]].append(edge[1])
graph[edge[1]].append(edge[0])
print(hasPath(graph, 'i','l', [])) # True
print(hasPath(graph, 'i','n', [])) # False
👇🏻 전체 코드 확인
https://github.com/Seeun-Lim/Algorithm
GitHub - Seeun-Lim/Algorithm: 알고리즘 공부하는 공간
알고리즘 공부하는 공간. Contribute to Seeun-Lim/Algorithm development by creating an account on GitHub.
github.com
'Python > [Algorithm] 알고리즘' 카테고리의 다른 글
| [Q2:English] First and last index in sorted array (0) | 2022.06.02 |
|---|---|
| [Q1:Korean] Anagram, 철자 확인 (0) | 2022.06.02 |
| Binary Search, 이진 탐색 (0) | 2022.05.18 |
| DFS & BFS (3) : 노드 탐색 (0) | 2022.04.28 |
| DFS & BFS (1) : 그래프 순회 (0) | 2022.04.26 |
